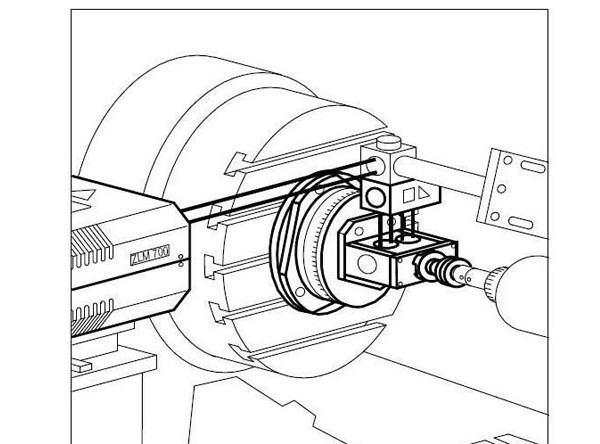
五轴数控机床为什么是五轴联动而非六轴联动呢？

在工科生脑海里通常会有这样一个概念：三维空间中的一个物体具有6个自由度。如下图所示：

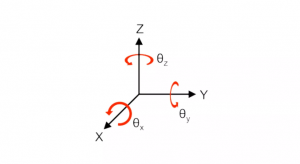
该坐标系为右手坐标系，这六个自由度分别为：沿着X、Y、Z三个轴的直线自由度；和绕着X、Y、Z三个轴的旋转自由度，旋转方向的正方向满足右手螺旋定则，见下图。

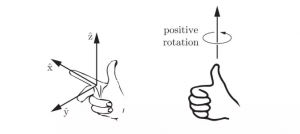
由于这个概念的影响，直观上，很可能会误以为“实现空间任意方向进行加工，机床就得拥有6个自由度或6个轴”。但事实是：空间物体有6个自由度，并不意味着能实现任意角度加工的机床就必须包含6个轴。这是问题的关键。

従来の三軸加工機では、複雑な加工面をもった部品や、穴がさまざまな方向にある製品を加工する際に、工具を任意の方向から加工物に当てるために特殊治具を用いたり、数回にわたって段取り替えを行っていた。しかし近年では、複雑形状部品を高速・高精度で加工できる同時五軸制御加工機が使われ始めている。[1]

传统的三轴机床在加工包含复杂表面或是具有各个方向孔的工件时，为了使得刀具从各个方向与工件接触，需要用到特殊的夹具，并且还要进行多次地工序变换。但使用五轴联动数控机床，可以实现在单次装夹下进行复杂形状工件的高速、高精密加工。

也就是说，刀具（或测头）可以从任意方向接近工件，才是机床实现任意角度加工的根本原因。

而机床是通过控制刀具（或测头）的位置和姿态来实现工件的加工（或测量）。因此，关键问题或者说前提是如何描述刀具（或测头）的位置和姿态。

三轴数控机床
在三轴数控机床的加工过程中，虽然刀具（或测头）的位置在不断变化，但是刀具（或测头）的姿态却是固定的。例如，一般立式三轴机床的刀轴方向在加工过程中一直沿着机床的Z轴的方向。通过X、Y、Z三个直线轴的坐标值即可完全确定刀具（或测头）的位置和姿态。[2]

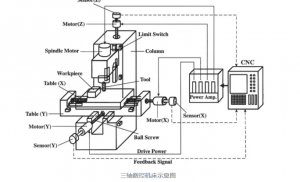
三轴数控机床示意图

五轴数控机床

通常情况下，五轴机床是在三轴机床的基础之上添加了两个旋转轴，通常用A、B、C轴来分别代表绕三个直线轴X、Y、Z、Y、Z的旋转轴。五轴机床包含A、B、C轴中的任意两个轴。

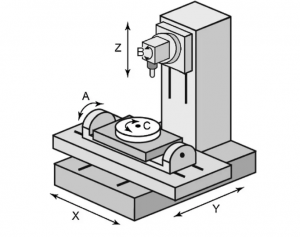
注意，上图只是想表达旋转轴和直线轴之间的关系，不要误以为上图是实际五轴机床的配置形式，实际五轴机床的旋转轴只包含上图A、B、C轴中的两个，即A、B轴，或A、C轴，或B、C 轴。在五轴加工中，由于这两个旋转轴的存在，导致刀具（或测头）的位置和姿态均会改变。显然，刀具（或测头）的位置在选定了主轴上的某个参考点后，可以通过三个直线轴X、Y、Z、Y、Z、Y、Z的坐标轴进行确定（当然，实际操作中还要考虑旋转中心到刀尖点的距离）。

但是刀具（或测头）姿态呢？

为了描述加工（或测量）过程中刀具（或测头）的姿态，就衍生出了“刀轴矢量”这个概念。刀轴矢量是一个三维的单位向量(i, j, k)，其中每个元素分别对应刀轴方向的单位向量在直线轴X、Y、Z、Y、Z、Y、Z三个方向的投影值。

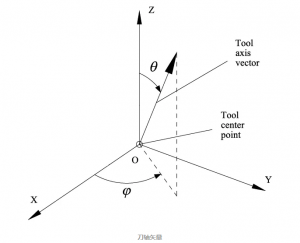
由于刀轴矢量是一个单位矢量，其模长为1。所以刀轴矢量的顶点在空间中的所有可能的位置构成了一个球面。

而任意的刀轴矢量方向，都可以通过由空间中的某个矢量绕着空间中两个不共线的轴旋转得到。

这样说有点抽象，但是我们生活中就有一个很好的例子——“经纬度”（其实也就是上图中的φ和θ角）。我们可以通过经纬度确定地球球面上的任意位置。经纬度仅仅包含两个坐标值，而这两个坐标值通过两个互相垂直的旋转轴的转角即可描述。

如下图，在确定球面上某个点的位置时（每个点都与一个刀轴矢量一一对应），可以通过两种坐标系描述。

采用左边的球面坐标系，也称球面坐标的显式表达（即，经纬度，包含两个坐标值，也就对应了两个自由度，因为经度和纬度之间是相互独立的）；

采用右边的直角坐标系，也称球面坐标的隐式表达（包含了三个坐标值，但依旧对应两个自由度，因为这三个坐标值之间包含一个隐性约束：X2+Y2+Z2=1 ）。[3]

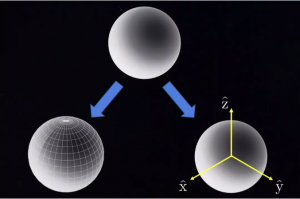
球面坐标的显式表达和隐式表达

所以，由两个旋转轴的旋转角度即可描述球面上一个确定的位置。而这个确定的球面位置点朝着直线轴X、Y、Z三个方向的投影值就是用来描述刀具（或测头）姿态的刀轴矢量。

这样，两个轴的旋转角度和刀轴矢量之间就建立了一一对应的关系。实际五轴加工中，数控系统根据数控程序中的刀轴矢量，通过运动学反解得到两个旋转轴各自的旋转角度，结合直线轴的坐标值，进而控制两个旋转轴和三个直线轴，使刀具（或测头）运动到预定的位姿（位置和姿态）。

用一个通俗但不太严谨的说法就是，只需要在三轴机床的基础之上再增加两个旋转轴（可以通俗理解为一个确定经度，一个确定维度），就能够控制刀具从空间中的任意方向接近被加工工件，实现任意复杂曲面的加工。

而在三轴机床的基础之上再增加两个旋转轴，并且能够依靠数控系统、伺服系统，以及RTCP（Rotation tool center point）等功能实现五轴联动加工的数控机床，自然就是五轴联动数控机床。[4]

关于欧拉角的补充

可能有人会类比图形学或机器人学，所以我觉得我有必要在最后补充一下，关于图形学中欧拉角的问题。

例如，在描述一个飞机的空间姿态时，会用到三个欧拉角，即yaw（偏航）、pitch（俯仰）和roll（翻滚），如下图。

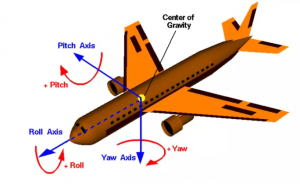
为什么描述飞机姿态需要考虑三个旋转角，而刀轴矢量却只需要考虑两个旋转角呢？

因为与描述飞机姿态不同的是，在描述刀轴矢量时，如果将绕刀轴方向定义为roll方向，则该roll方向的角度我们是不关心的。换句话说，刀具绕主轴的旋转并不会影响刀轴矢量，只需要靠yaw和pitch就能得到所谓的经纬度了。这也是为什么描述刀轴矢量只要两个自由度。

希望最后这段解释能够帮助相关领域的人理解这之间的区别。

Reference

Sakamoto, S., & Inasaki, I. (1993). Analysis of generating motion for five-axis machining centers. Transactions of the Japan Society of Mechanical Engineers Series C, 59(561), 1553–1559. https://doi.org/10.1299/kikaic.59.1553

Altintas, Y. (2012). Manufacturing Automation: Metal Cutting Mechanics, Machine Tool Vibrations, and CNC Design. Applied Mechanics Reviews (Vol. 54). https://doi.org/10.1115/1.1399383

Modern Robotics: Mechanics, Planning, and Control http://hades.mech.northwestern.edu/index.php/Modern_Robotics

Moriwaki, T. (2008). Multi-functional machine tool. CIRP Annals, 57(2), 736–749. https://doi.org/10.1016/J.CIRP.2008.09.004